Obwohl es große Unterschiede in der Art der Wartungsarbeiten in Industrieanlagen gibt, enthält es Prozesse, bei denen ähnliche Größen wie z. Vibration, Temperatur, Ölqualität usw. werden gemessen. Während dieser Prozesse werden Daten von Sensoren mit Wandlern in verschiedene Einheiten umgewandelt und Kommentare zum Systemzustand abgegeben. RMS (Root Mean Square) wird im Allgemeinen bei der Schwingungsanalyse verwendet. Es wird häufig verwendet, da das RMS-Schwingungsprofil Aufschluss über den Energiegehalt und damit die Zerstörungskapazität der Schwingung gibt. Es ist jedoch nicht korrekt, mit einem einzigen Parameter Rückschlüsse auf das System zu ziehen.
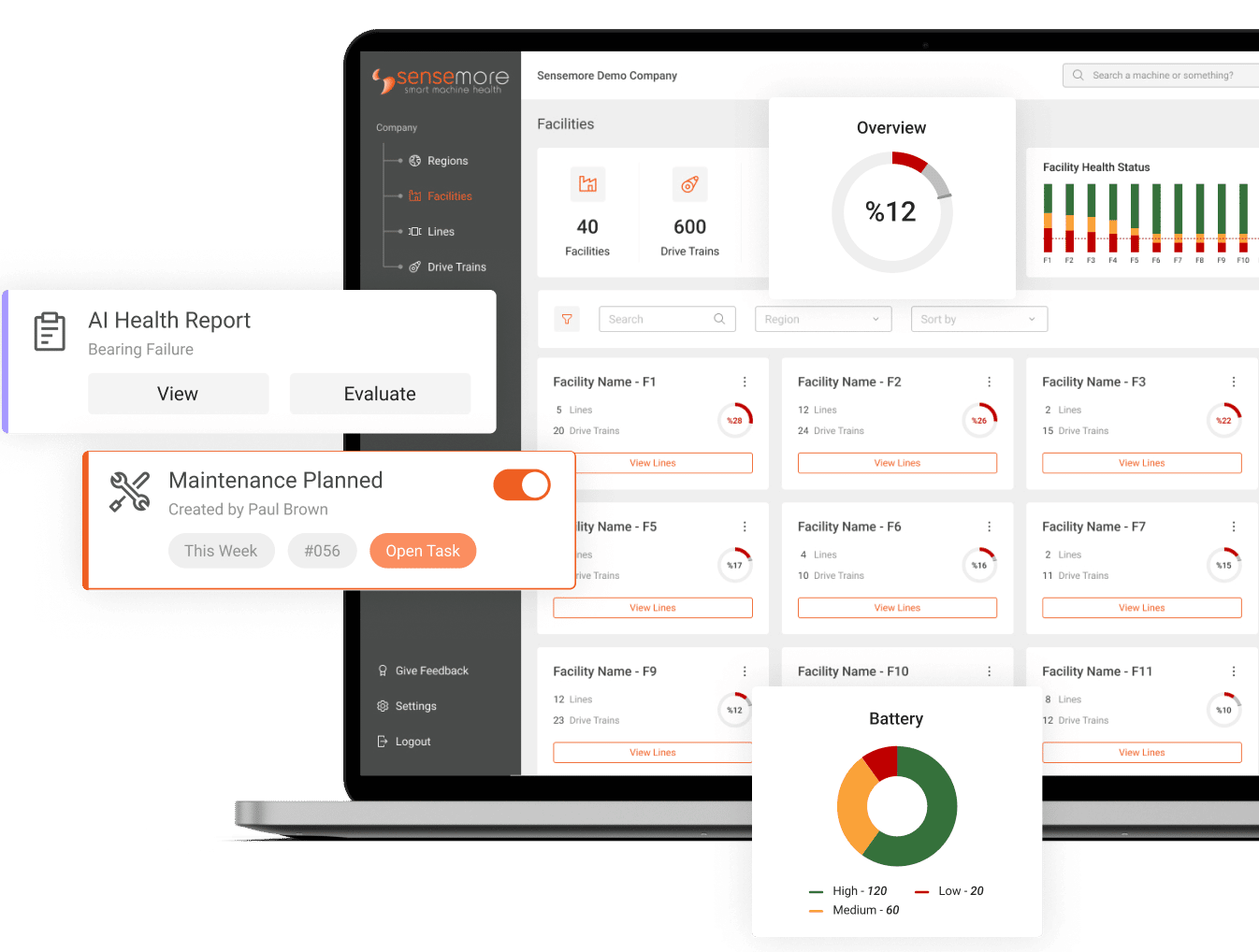
Daher werden bei der Fehlerbehebung verschiedene Parameter verwendet, und ein Ansatz mit mehreren Parametern liefert die besten Ergebnisse, um die Grundursache des Problems zu ermitteln. Sensemore stellt Ausgaben bereit, indem es dieses Verfahren mit verschiedenen Parametern in seiner Schnittstelle für eine genaue Erkennung bei der Vibrationsanalyse übernimmt und dem Benutzer gleichzeitig ermöglicht, verschiedene Telemetriedaten hinzuzufügen.
Der größte Vorteil der Schwingungsanalyse besteht darin, dass sie sich entwickelnde Probleme an Maschinen und Anlagen erkennen kann, bevor sie zu schwerwiegend werden und zu Ausfallzeiten führen. Dies lässt sich erreichen, indem die Maschine Vibrationen regelmäßig oder in bestimmten Zeitabständen überwacht werden. Die Fehlererkennung kann auf verschiedene Arten erfolgen. Wir können die Methoden der vorausschauenden Wartung unter zwei Hauptüberschriften untersuchen:
- Zeitwellenformanalyse
- Frequenzbereichsanalyse
Zeitwellenformanalyse
Die Wellenform entsteht, wenn das Vibrationssignal von einem Beschleunigungsmesser erfasst und dann in ein digitales Signal umgewandelt und anschließend abgebildet wird. Dieses Signal liegt im Zeitbereich. Der Zeitbereich ist die aufgetragene Amplitude über der Zeit. Während das Vibration Problem bei den meisten Maschinen mithilfe der Spektrumanalyse erkannt wird, können einige Arten von Wellenformen auch effektiv zur Verbesserung der Spektralinformationen genutzt werden. Die Zeitwellenform kann effektiv für Anwendungen mit niedriger Drehzahl verwendet werden, um die Schwere von Lagerausfällen zu beurteilen, die tatsächliche Amplitude anzuzeigen und die Spektralinformationen in Situationen zu verbessern, in denen Lockerheit und Schläge auftreten.
Wälzkörper in Wälzlagern erzeugen periodische Effekte, wenn sie auf einen kleinen Riss oder Verschleiß stoßen. Wenn externes Rauschen vorhanden ist, weist das Spektrum dieses Signals möglicherweise keinen genau definierten Peak auf, aber wenn eine Beschleunigung auftritt, bilden sich normalerweise Peaks mit Wiederholungsraten, die der defekten Frequenz des Laufrings oder der Frequenzperiode der Lagerkugelpassfrequenz entsprechen.
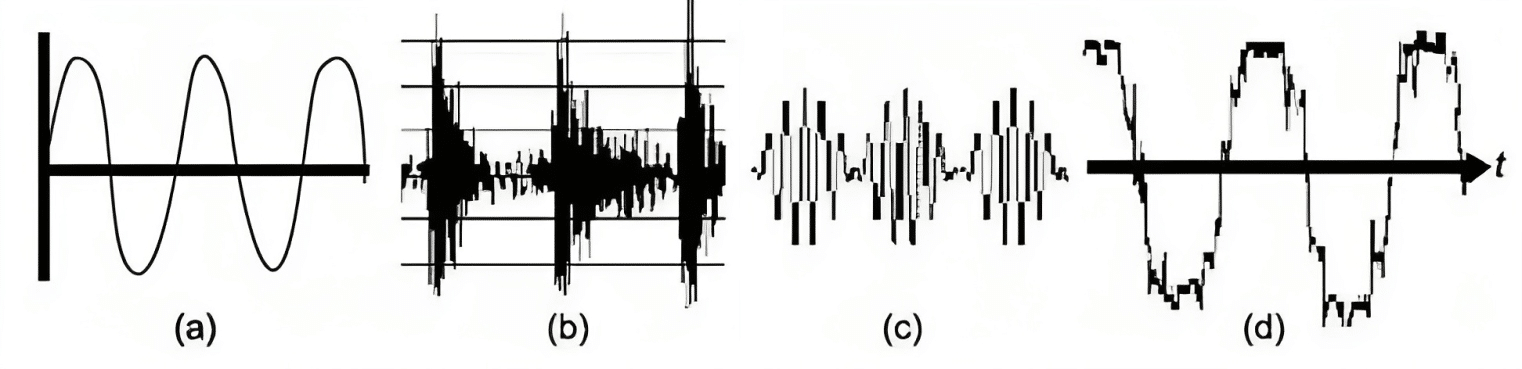
Abb. 1 Typische Fehler a) Unwucht b) Beschädigung des Außenrings c) Schwebungsphänomen d) Lockerheit
Wenn zwei oder mehr benachbarte Maschinen mit annähernd gleicher Geschwindigkeit arbeiten, kommt es zu Schwebungen mit den aktuellen Summen- und Differenzfrequenzen. Die Schwebungsfrequenz ist im Spektrum möglicherweise nicht deutlich sichtbar, da sie einer außergewöhnlich niedrigen Frequenz entspricht. Allerdings ist es in der Zeitaufzeichnung deutlich als amplitudenmoduliertes Signal zu erkennen.
In vielen Fällen von Lockerheit, beispielsweise wenn sich ein Lagerblock während eines Teils der Drehung leicht anhebt, was die Vibration verursacht, und dann für den Rest des Zyklus die Basis berührt, flacht die Wellenform über einem bestimmten Wert ab. Sie manifestiert sich im Spektrum als Harmonische, die nicht von anderen Arten von Wellenformverzerrungen zu unterscheiden sind, die ebenfalls Harmonische erzeugen. Eine solche Lockerheit, bei der die Bewegung der Zeitwellenform in eine Richtung eingeschränkt ist, kann schnell erkannt werden.
Wenn eine lose Maschinenkomponente mit einer Geschwindigkeit auf ein Gerät trifft, die nichts mit der Maschinengeschwindigkeit zu tun hat, erzeugt sie zufällige Vibrationen, die oft nicht periodisch sind. Obwohl dieses Spektrum anderen Breitbandrauschquellen ähnelt, sind die Auswirkungen in der Zeitbereichswellenform sehr deutlich sichtbar.
Aus der Zeitaufzeichnung eines Vibrationssignals können einige Indizes extrahiert werden, die für die Diagnose nützlich sind. Die am häufigsten verwendeten Indizes sind statistische Parameter, die aus dem Rohsignal berechnet werden können, um Unterschiede zwischen Protokollen hervorzuheben und sie für Diagnose und Trend nützlich zu machen. Da diese Parameter von den Vibrationen aller Komponenten der Maschine beeinflusst werden, können sie das fehlerhafte Bauteil in der Maschine zwar nicht genau identifizieren, ermöglichen aber ein Vorgehen gegen Störungen. Einige dieser Parameter sind RMS, Crest-Faktor, Schiefe, Kurtosis-Faktor und Clearance-Faktor. Die regelmäßige Erstellung dieser Funktionen (Trendverfolgung) ist eine gängige Technik zur Situationsüberwachung. Die Tatsache, dass diese Eigenschaften erheblich von den Referenz- oder Basiswerten (gemessen unter normalen Bedingungen) abweichen, ist ein Hinweis darauf, dass im System Fehlfunktionen vorliegen.
Der RMS-Wert wird unter Berücksichtigung des Zeitverlaufs der Welle berechnet. Es ist ein Maß für den Energiegehalt im Schwingungszeichen und damit einer der genauesten statistischen Parameter für die Schwere eines Maschinenausfalls. Diese Funktion eignet sich gut zur Überwachung des gesamten Vibrationspegels, liefert jedoch keine Informationen darüber, welche Komponente fehlerhaft ist. Der RMS-Wert kann bei der Erkennung einer großen Unwucht in rotierenden Anlagensystemen äußerst effektiv sein. Mit dem Auftreten von Stoßimpulsen erhöht sich auch der RMS-Wert. Mit den folgenden Gleichungen können RMS-Werte für diskrete und kontinuierliche Zeitsignale berechnet werden.
Der Crest-Faktor ist definiert als das Verhältnis des Spitzenwerts einer Wellenform zu ihrem RMS-Wert und ist daher eine dimensionslose Größe. Der Ausdruck rechts definiert den Crest-Faktor. Der Scheitelfaktor einer Sinuswelle beträgt 1,414. Wenn ein typisches Vibrationssignal von einer Maschine mit großer Unwucht empfangen wird, stellt dies kein weiteres Problem dar. Ein Scheitelfaktor von 1,5 wird erreicht, während der Scheitelfaktor viel größer wird, wenn die Lager zu verschleißen beginnen und es zu Stößen kommt. Die Grundlage des Ansatzes besteht darin, dass bei einem Lagerausfall die
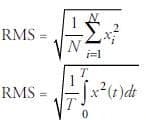
Abb. 2 RMS-Formel
Beschleunigungsspitzen aufgrund der zunehmenden Impulsivität schneller ansteigen als die RMS-Werte. Der Scheitelfaktor lässt sich leicht berechnen und ist relativ unempfindlich gegenüber Lagergeschwindigkeit und -last. Im Anfangsstadium eines Lagerschadens können der Innenring des Lagers, das Lagergehäuse, die Wälzkörper und der Käfig periodische Stoßsignale erzeugen. Dadurch erhöht sich der Crest-Faktor-Wert. Wenn sich der Schaden jedoch verschlimmert, steigt der RMS-Wert und führt zu einer Verringerung des Crest-Faktor-Werts.
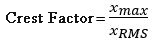
Abb. 3 Wappenformel
Die Schiefe misst das Asymmetrieverhalten des Schwingungssignals durch die Wahrscheinlichkeitsdichtefunktion. Die Schiefe einer Verteilung wird als das Fehlen von Symmetrie definiert. Die Schiefe ist ein dimensionsloses Maß und misst, wie unsymmetrisch das Signal um den Mittelwert ist. Wenn das Signal symmetrisch ist, ist die Schiefe Null. Bei den meisten Vibrationssignalen ist die Wahrscheinlichkeitsverteilung wie die Normalverteilung symmetrisch zum Mittelwert. Daher weist ein Versatz ungleich Null in den meisten Fällen darauf hin, dass etwas nicht stimmt.
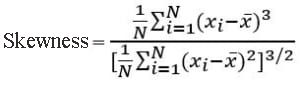
Abb. 4 Schiefeformel
Der Kurtosis-Faktor ist ein statistischer Indikator zur Charakterisierung des Pulszustands eines Signals. Ein hoher Kurtosis-Faktor weist auf das Vorhandensein sich wiederholender Impulse hin. Es trägt dazu bei, festzustellen, ob das Spektrum kleine, über einen weiten Frequenzbereich verstreute Peaks oder nur wenige Peaks an bestimmten Orten enthält.
Es eignet sich besonders für die Überwachung der Lager langsam rotierender Wellen, bei denen frequenzbasierte Techniken nur begrenzt möglich sind. Kurtosis wird auch häufig zur Erkennung nichtperiodischer Schocks eingesetzt. Der Kurtosis-Faktor einer normalen Peilung beträgt 3. Signale mit einem größeren Kurtosis-Wert weisen mehr Spitzen auf; Dies sind die Spitzen, die größer als das Dreifache des Effektivwerts des Signals sind.
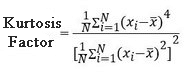
Abb. 5 Kurtosis-Faktor
Frequenzbereichsanalyse
Zeitsignale lassen sich mithilfe mathematischer Transformationen einfacher interpretieren, um verarbeitete Signale zu erhalten, die Informationen offenbaren, die im Rohsignal nicht leicht sichtbar sind. Die häufigste davon ist die Konvertierung in den Frequenzbereich. Der Zeitbereich wird in den Frequenzbereich umgewandelt, indem die Fourier-Transformation auf das Vibrationssignal angewendet wird. Bei dieser Methode wird die Energie im Originalsignal in verschiedene Frequenzkomponenten aufgeteilt und die Amplitude-Frequenz-Darstellung dieses Signals erhalten. Der Hauptvorteil dieses Formats besteht darin, dass jede Periodizität im Schwingungssignal deutlich als Spitzen im Spektrum bei entsprechenden Frequenzen angezeigt wird.
Dies ermöglicht eine frühzeitige Erkennung von Fehlern, die häufig bestimmte charakteristische Frequenzkomponenten im Vibrationssignal erzeugen und sich im Laufe der Zeit verschlechtern, wenn sich die Situation verschlechtert. Der Nachteil der Frequenzbereichsanalyse besteht jedoch darin, dass während des Konvertierungsprozesses eine erhebliche Menge an Informationen (Übergänge, sich nicht wiederholende Signalkomponenten) verloren gehen kann. Diese Technik ist die am weitesten verbreitete Technik in der Maschinendiagnose und 85 % der mechanischen Probleme in rotierenden Geräten können erkannt werden.
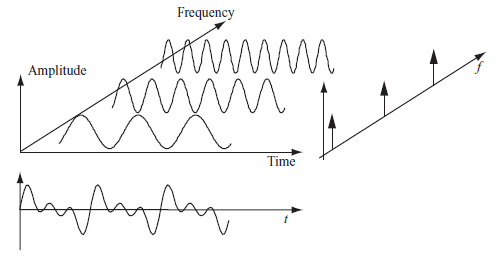
Abb. 6 Signalansicht aus Zeit- und Frequenzdomänen
Jedes Gerät, aus dem die Maschinen bestehen, weist charakteristische Frequenzen gegenüber der angetriebenen Kraft auf. Diese Frequenzen werden auch bei der Diagnose von Maschinenausfällen verwendet. Verschiedene Störungen erzeugen spezifische Spektren. Nachdem die in Zeitform empfangenen Signale in den Frequenzbereich umgewandelt wurden, können sie mit charakteristischen Fehlerspektren verglichen werden und es kann eine Interpretation darüber vorgenommen werden, um welches Gerät es sich handelt und warum der Fehler aufgetreten ist.
Die Merkmale des Ausfalls sind die Drehzahl des rotierenden Elements, die Übergangsfrequenzen zwischen Innen- und Außenring des Lagers, die Frequenz des Zahnradnetzwerks usw. und bestimmen gerätespezifische Frequenzen. Wenn wir beispielsweise das Problem der parallelen Fehlausrichtung in einem Motor-Pumpen-System untersuchen, das durch eine Kupplung miteinander verbunden ist, tritt im Spektrum ein radialer Peak bei der Motordrehfrequenz auf. Während beim 2. und 3. Zeitpunkt der Motordrehfrequenz Spitzen auftreten, ist überwiegend die 2. Harmonische zu erkennen. Dieses Spektrum kann jedoch auch zu Beginn der Störung beobachtet werden.
Um die Schwere der Situation zu messen, werden die Amplitudenwerte der charakteristischen Frequenzen verwendet, aus denen sich der Fehler zusammensetzt. Auf diese Weise können anhand verschiedener Standards Schwellenwerte festgelegt werden, die den Schweregrad der Situation aufzeigen. Daher betrachten wir im Spektrum die Frequenzachse, um die Ursache des Fehlers zu finden, und die Amplitudenachse, um die Schwere des Fehlers zu bestimmen.
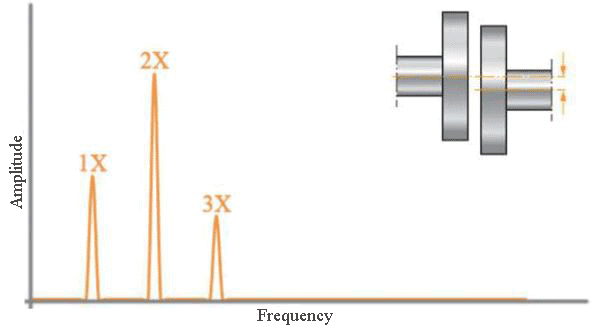
Abb. 7 Charakteristisches paralleles Fehlausrichtungsspektrum
Sensemore bietet verschiedene Lösungen für die Schwingungsanalyse im Zeitwellenform- und Frequenzbereich. Sie können die rohen G-Daten, die Sie vom Beschleunigungssensor erhalten, im GRMS- und VRMS-Format beobachten.
Sie können Alarme erstellen, indem Sie den Trend der periodischen Messungen Ihrer Geräte in Bezug auf Gesamt-GRMS, VRMS und Temperaturwerte im Zeitverlauf beobachten. Sie können diese Alarme auch per E-Mail oder mobiler Benachrichtigung erhalten. Es ermöglicht Ihnen, die Situation zu überwachen, indem Sie Trends anhand verschiedener statistischer Parameter wie Crest-Faktor, Kurtosis und Schiefe erstellen, um Ihre Daten im Zeitbereich einfacher zu analysieren. Bei der Spektrumanalyse können Sie ganz einfach die Harmonischen der spitzenbildenden Frequenzen beobachten und Vergleiche mit den gängigen Fehlerspektren in unserer Bibliothek anstellen.
Abb. 8 Sensemore LAKE Facility Dashboard
References:
- C. Scheffer, P. GirdharMachinery Vibration Analysis & Predictive Maintenance(Oxford:Elsevier, 2004) –
- A. Brandt, Noise and Vibration Analysis(New Delhi: Wiley, 2011)
- C. Sujatha, Vibration and Acoustics(New Delhi:Mc Graw Hill Education, 2010)
Weiterführende Literatur
Dezember 28, 2022
KI-gestützte Fehlerdiagnose mit Modusähnlichkeitsanalyse
AI can diagnose machine faults with vibration data but machine mode similarity analysis is an alternative, it uses…
September 15, 2022
Daten zu rotierenden Maschinen verstehen
Maschinendaten werden durch physische Attribute und Aktionen von Maschinen generiert, von Sensoren gesammelt und…
August 6, 2021
Hüllkurvenanalyse
Bearings are critical elements in rotating machines, they support radial and axial loads, and reduce friction. Real…
Mai 6, 2021
Was ist Cepstral-Analyse?
Die Cepstral-Analyse, ein Werkzeug zur Erkennung von Periodizität im Frequenzspektrum, kann bei der Erkennung von…
September 21, 2020
Parameterauswahl in der Vibrationsmessung
Vibrationsmessungen werden verwendet, um die Reaktion von Maschinen auf Kräfte zu bestimmen und potenzielle Probleme zu…
September 4, 2020
Was ist Schwingungsanalyse?
Um die Schwingungsanalyse zu verstehen, ist es wichtig, zunächst das Konzept der Schwingung selbst zu verstehen.…