In mechanischen Systemen können verschiedene Teile derselben Ausrüstung aufgrund von Unterschieden in Form, Materialien und anderen Faktoren unterschiedliche Vibrationen aufweisen. Zum Beispiel können in einem Förderband-System mit einem Elektromotor und einem Reduzierer die Vibrationen an der Ausgangswelle des Reduzierers bei hohen Frequenzen ganz anders sein als die des Elektromotors. Die Verwendung derselben Parameterauswahl bei der Vibrationsmessung an beiden Teilen kann zu inkorrekten Ergebnissen führen.
Die Rolle der Stichprobengröße und der Abtastrate für Parameterauswahl
Die Rolle der Stichprobengröße und der Abtastrate für Parameterauswahl Bei der Umwandlung eines Analogsignals in ein digitales (ADC) ist die Größe der Proben des digitalen Wellenforms entscheidend, um das Analogsignal genau zu replizieren. Vibrationsmessungen erstrecken sich normalerweise über einen Zeitraum und erfolgen in regelmäßigen Abständen. Das Analogsignal wird in digitaler Form durch Proben genommen, die zu bestimmten Zeitintervallen als Abtastzeit (1/fs) bekannt sind.
Die Anzahl der Proben, die pro Sekunde genommen werden, wird als Abtastrate oder Abtastrate bezeichnet. Es ist wichtig zu beachten, dass das Intervall zwischen periodischen Messungen durch die Division der Probenanzahl durch die Abtastfrequenz bestimmt wird. Die Hälfte der Abtastfrequenz (fs/2) wird als Nyquist-Frequenz bezeichnet.
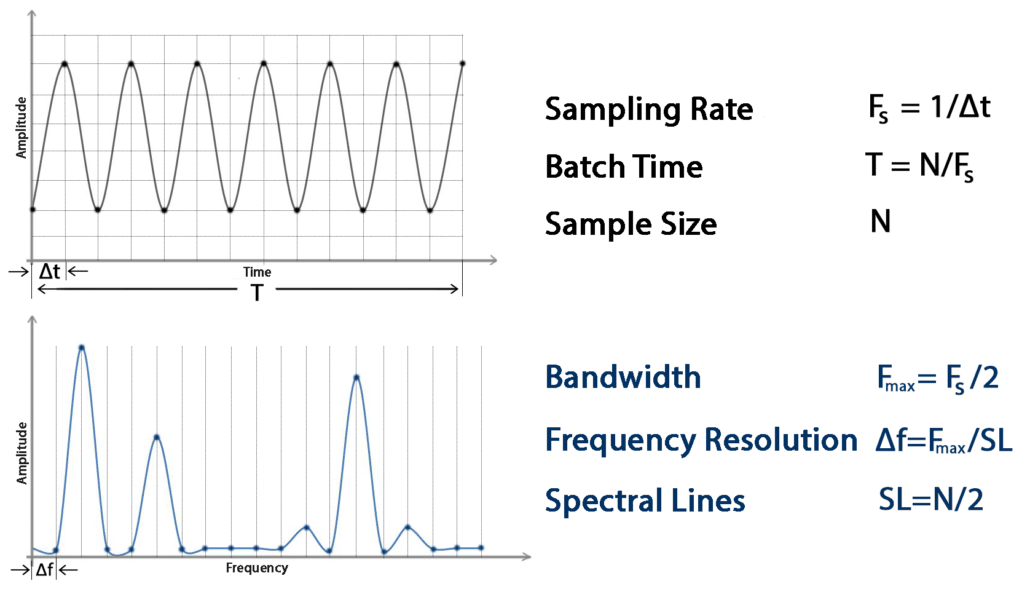
Abb. 1 Zeit- und Frequenzbereichsparameter
Das Nyquist-Shannon-Abtasttheorem
Analoge Signale bestehen aus Komponenten mit unterschiedlichen Frequenzen. Die höchstfrequente Komponente, bezeichnet als fmax, definiert die Bandbreite des Signals. Gemäß dem Nyquist-Shannon-Abtasttheorem sollte die Abtastfrequenz mindestens das Doppelte der höchsten Frequenzkomponente im analogen Signal betragen, also 2×fmax. Dieses Theorem betont die Bedeutung des Verständnisses der Auswirkungen der Abtastfrequenz. Wenn Sie dieses Theorem vor der Abtastung eines analogen Signals befolgen, repräsentiert das abgetastete Signal genau das analoge Signal und bewahrt alle seine Informationen. Wenn jedoch die Abtastfrequenz unter 2-mal der höchsten Frequenz im analogen Signal liegt (fs<2×fmax), tritt Aliasing auf. Aliasing versteckt hohe Frequenzen im Spektrum des analogen Signals und kann zu Fehlinterpretationen der Signale führen, die von der Vibrationsquelle erzeugt werden.
Einfluss der Abtastfrequenz auf die Spektrumbreite
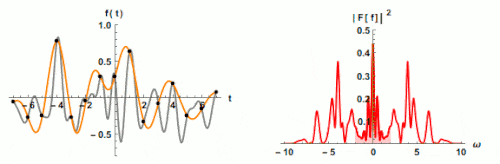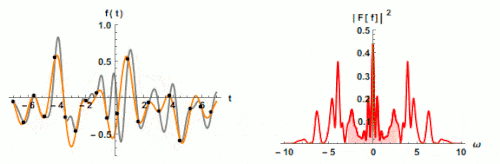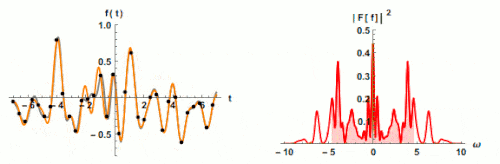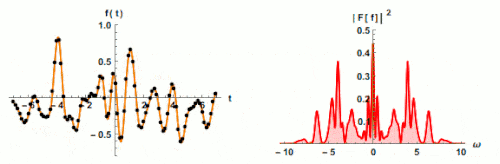
Fig. 2 The Effect of Sampling Rate on Spectrum Bandwidth
Wenn wir das Abtasttheorem nicht befolgen, tritt ein Phänomen namens Aliasing auf. Im Falle von Aliasing werden analoge Signale auf eine andere Weise in digitale Signale umgewandelt, was verhindert, dass hohe Frequenzen im Spektrum erscheinen. Daher ist Aliasing ein unerwünschtes Phänomen bei der Verarbeitung digitaler Signale. Alle Datenkollektoren/Analysatoren verfügen über integrierte Abtastraten, um Aliasing zu vermeiden.
Theoretisch sollte es keine Vibrationen mit einer Frequenz von mehr als der Hälfte dieser Abtastrate geben. Dies kann jedoch in der Praxis niemals erreicht werden. Deshalb verfügen alle Analysatoren über Anti-Aliasing-Filter. Dies sind Tiefpass-Elektronikfilter, die niedrigere Frequenzen passieren lassen, aber höhere blockieren. Die Filter eliminieren alle Vibrationen in einem analogen Signal mit Frequenzen größer als der Hälfte der Abtastfrequenz. Diese Filter passen sich automatisch den entsprechenden Werten an, wenn sich die Abtastfrequenz ändert. Dies geschieht, wenn der Frequenzbereich des Analysators vom Benutzer geändert wird.
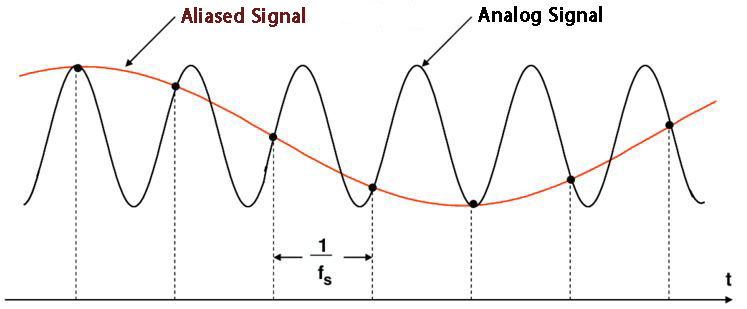
Abb. 3 Aliasing
Diskrete Darstellung von analogen Signalen
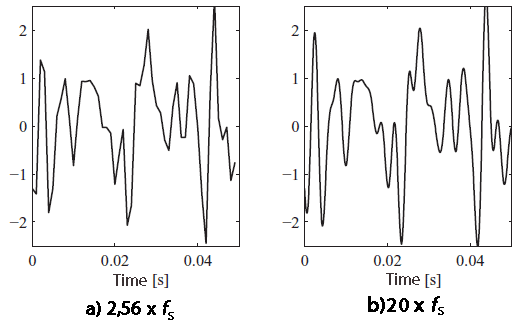
Viele für Vibrationsignale konzipierte Messsysteme verwenden begrenzte Hochgeschwindigkeitsabtastraten, die die Genauigkeit der erzeugten Zeitsignale beeinflussen können. Wenn die Abtastrate viel niedriger ist (z. B. 2,56-mal niedriger) als die Frequenz des analogen Signals, wird oft Oversampling (z. B. 20-mal) angewendet, um dies auszugleichen. Trotz der niedrigeren Abtastrate ist es entscheidend zu verstehen, dass das Signal immer noch alle Informationen des analogen Signals enthält. Obwohl das Signal zwischen den Abtastpunkten bei einer niedrigeren Frequenz zu springen scheint, bleibt seine Integrität im Frequenzbereich intakt. Das bedeutet, dass ein aus dem Signal berechnetes Spektrum genau bleibt. Die durch die niedrige Abtastrate auferlegte Einschränkung betrifft hauptsächlich die zeitbasierte Darstellung des Signals, nicht die frequenzbasierte.
Auswirkungen der Abtastrate auf die Signalrepräsentation
Wenn die Abtastrate unter die erforderliche Schwelle fällt (fs<2×fmax), tritt Aliasing auf und beeinträchtigt die Integrität des Signals. Das bedeutet, dass Hochfrequenzkomponenten im analogen Signal in der digitalen Darstellung möglicherweise nicht korrekt erscheinen. Aliasing ist ein Phänomen, das wir vermeiden wollen, um genaue Vibrationsmessungen zu erhalten.
Auswahl des richtigen Dynamikbereichs
Neben der Abtastrate ist ein weiterer entscheidender Aspekt bei der Messung von Vibrationen der Dynamikbereich. Der Dynamikbereich bezieht sich auf die Fähigkeit des Messsystems, eine breite Palette von Vibrationsamplituden genau zu erfassen. Unterschiedliche Maschinen und Anwendungen zeigen unterschiedliche Niveaus der Vibrationsintensität.
Um die Bedeutung des Dynamikbereichs zu verdeutlichen, nehmen Sie an, Sie messen Vibrationen von einer Maschine. In einigen Fällen können diese Vibrationen relativ gering sein, ähnlich einem sanften Summen, und fallen in einen niedrigen Bereich (z. B. 2G). In anderen Fällen können die Vibrationen jedoch viel intensiver sein, ähnlich kraftvollen Erschütterungen, was einen höheren Dynamikbereich erfordert (z. B. 8G oder 16G).
Die Konsequenzen der Auswahl eines falschen Dynamikbereichs
Wenn Sie sich für einen Dynamikbereich entscheiden, der für die tatsächlichen Vibrationsamplituden zu begrenzt ist, besteht die Gefahr des „Clippings“ der Daten. In einfacheren Worten verlieren Sie Informationen über die tatsächliche Intensität der Vibration, ähnlich wie der Versuch, das Brüllen eines Löwen mit einem Mikrofon aufzunehmen, das nur Flüstern erfassen kann.
Andererseits kann die Auswahl eines übermäßig breiten Dynamikbereichs für relativ geringe Vibrationsintensitäten zu einer Verringerung der Empfindlichkeit führen. Es ist vergleichbar mit der Verwendung eines Mikroskops zum Lesen von Großdruck; Sie könnten feinere Details übersehen.
Automatische Anpassung von Anti-Aliasing-Filtern
Um die Herausforderungen durch Aliasing aufgrund unzureichender Abtastraten zu mildern, integrieren die meisten Datenkollektoren und Analysatoren Anti-Aliasing-Filter. Diese Filter passen sich automatisch an Änderungen in der Abtastrate an, verhindern Aliasing und gewährleisten die Integrität der Daten.
Verweise
- C. Scheffer, P. GirdharMachinery Vibration Analysis & Predictive Maintenance(Oxford:Elsevier, 2004)
- A. Brandt, Noise and Vibration Analysis(New Delhi: Wiley, 2011)
- Bertoletti, 2020, Nyquist-Shannon Sampling Theorem
Weiterführende Literatur
Dezember 28, 2022
KI-gestützte Fehlerdiagnose mit Modusähnlichkeitsanalyse
AI can diagnose machine faults with vibration data but machine mode similarity analysis is an alternative, it uses…
September 15, 2022
Daten zu rotierenden Maschinen verstehen
Maschinendaten werden durch physische Attribute und Aktionen von Maschinen generiert, von Sensoren gesammelt und…
August 6, 2021
Hüllkurvenanalyse
Bearings are critical elements in rotating machines, they support radial and axial loads, and reduce friction. Real…
Mai 6, 2021
Was ist Cepstral-Analyse?
Die Cepstral-Analyse, ein Werkzeug zur Erkennung von Periodizität im Frequenzspektrum, kann bei der Erkennung von…
Oktober 9, 2020
Wie erfolgt die Fehlererkennung?
Vibrationsmessungen und -analysen unter Verwendung mehrerer Parameter können sich entwickelnde Probleme in Maschinen…
September 4, 2020
Was ist Schwingungsanalyse?
Um die Schwingungsanalyse zu verstehen, ist es wichtig, zunächst das Konzept der Schwingung selbst zu verstehen.…
Sensemore Predictive Maintenance-Lösung
Wenn Ihnen dieser Blog gefallen hat, erkunden Sie unsere Seite zur vorausschauenden Wartungslösung.