Parameter selection in vibration measurement means choosing the sampling rate, sample size and dynamic range that match the equipment being measured, because different parts of the same machine vibrate differently and a single set of parameters can give incorrect results. For example, in a conveyor system with an electric motor and a reducer, the vibrations in the reducer’s output shaft may be quite different from those of the electric motor when it runs at high frequencies. This article explains how sample size and sampling rate are defined, what the Nyquist-Shannon sampling theorem and aliasing mean in practice, how anti-aliasing filters work, and how to select the right dynamic range.
The Role of Sample Size and Sampling Rate for Parameter Selections
In the process of turning an analog signal into a digital one (ADC), the size of the digital waveform’s samples is vital for accurately replicating the analog signal. Vibration measurements usually cover a period of time and are taken at regular intervals. The analog signal is transformed into digital format through samples taken at specific time intervals known as the sampling time (1/fs). The number of samples taken each second is called the sampling rate or sampling frequency. It’s important to remember that dividing the sample size by the sampling frequency (T = N/fs) gives the duration of one measurement record, and that the line resolution of the resulting spectrum is its reciprocal (Δf = fs/N). How often periodic measurements are repeated is a scheduling decision and is unrelated to N and fs. Half of the sampling frequency (fs/2) is referred to as the Nyquist Frequency.
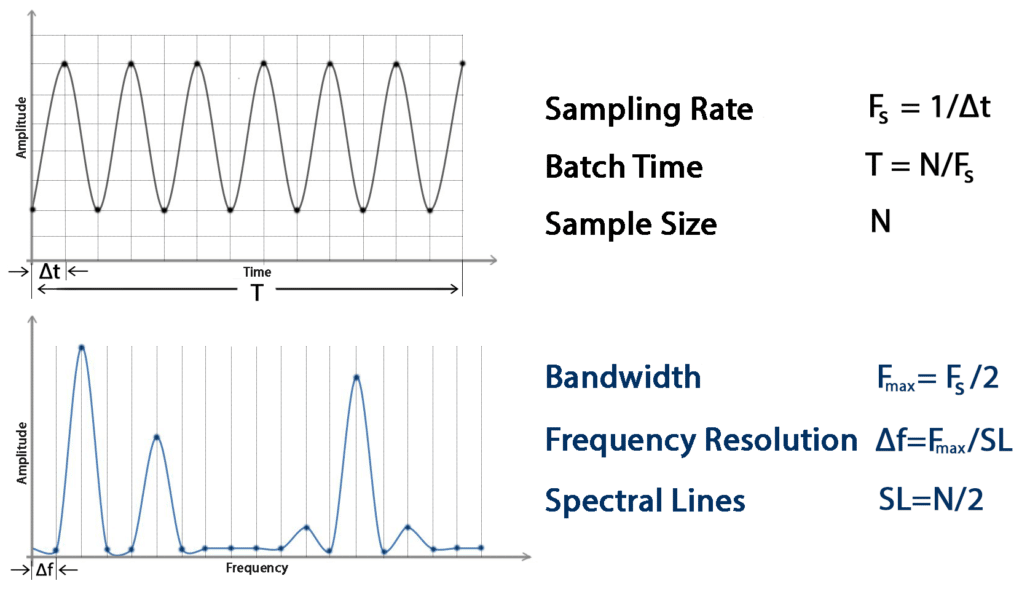
Fig. 1 Time and Frequency Domain Parameters
The Nyquist-Shannon Sampling Theorem
Analog signals consist of components at different frequencies. The highest-frequency component, denoted as fmax, defines the signal’s bandwidth. As per the Nyquist-Shannon Sampling Theorem, the sampling rate should be at least twice the highest frequency component in the analog signal, or 2×fmax. This theorem emphasizes the importance of understanding the implications of the sampling rate. When you follow this theorem before sampling an analog signal, the sampled signal accurately represents the analog signal, preserving all its information. However, if the sampling frequency falls below 2 times the highest frequency in the analog signal (fs<2×fmax), aliasing occurs. Aliasing folds the components above the Nyquist frequency back into the analyzed band, where they show up as false low-frequency peaks, and can lead to misinterpretations of the signals produced by the vibration source.
Effect of Sampling Rate on Spectrum Bandwidth
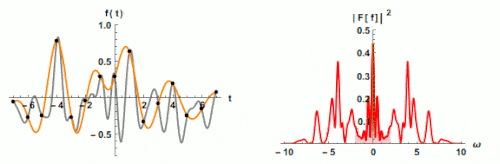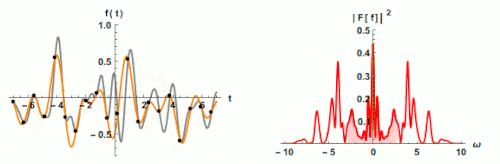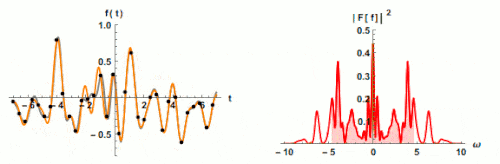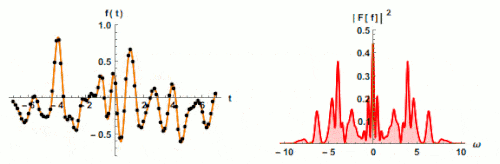
Fig. 2 The Effect of Sampling Rate on Spectrum Bandwidth
If we do not follow the sampling theorem, a phenomenon called aliasing is going to occur. In case of aliasing, the components above the Nyquist frequency are folded back into the analyzed band, where they appear as false low-frequency peaks that cannot be told apart from real ones. Therefore, aliasing is an undesirable phenomenon in which digital signals are processed. All data collectors/analyzers have built-in sampling rates to avoid aliasing. Theoretically, there should be no vibrations with a frequency more than half of this sampling rate. However, this can never be achieved in practice. That is why all analyzers have anti-aliasing filters. These are low-pass electronic filters that allow lower frequencies to pass but block higher ones. Filters eliminate all vibrations in an analog signal with frequencies greater than half the sampling rate. These filters automatically adjust to the appropriate values as the sampling frequency changes. This happens when the analyzer’s frequency range is changed by the user.
Fig. 3 Aliasing
Discrete Representation of Analog Signals
Many measurement systems designed for vibration signals use limited high-speed sampling rates, which can affect the accuracy of time signals generated. In practice, analyzers sample at 2.56 times the maximum analysis frequency (fs = 2.56 × fmax). This margin above the theoretical minimum of 2 × fmax leaves room for the roll-off of the anti-aliasing filter. Because the Nyquist criterion is met, it’s crucial to understand that the record still contains all the information the analog signal carries within the analyzed band. While the waveform may look coarse and seem to jump between sampling points, its integrity remains intact in the frequency domain. This means that a spectrum calculated from the signal remains accurate. The limitation imposed by the finite sampling rate primarily affects the time-based representation of the signal, not the frequency-based one.
Impact of Sampling Rate on Signal Representation
When the sampling rate falls below the required threshold (fs<2×fmax), aliasing occurs, distorting the signal’s integrity. This means that high-frequency components in the analog signal reappear in the digital representation at the wrong, lower frequencies. Aliasing is a phenomenon we want to avoid to obtain accurate vibration measurements.
Selecting the Right Dynamic Range
Aside from sampling rate, another crucial aspect to consider is the dynamic range when measuring vibration. Dynamic range refers to the ability of the measurement system to capture a wide range of vibration amplitudes accurately. Different machinery and applications exhibit varying levels of vibration intensity. To illustrate the importance of dynamic range, consider a scenario where you’re measuring vibrations from a machine. In some cases, these vibrations may be relatively small, akin to a gentle hum, and fall within a low range (e.g., 2G). However, in other instances, the vibrations might be much more intense, resembling powerful jolts, necessitating a higher dynamic range (e.g., 8G or 16G).
The Consequences of Choosing the Wrong Dynamic Range
If you opt for a dynamic range that’s too limited for the actual vibration amplitudes, you risk “clipping” the data. In simpler terms, you’ll lose information about the vibration’s actual intensity, like trying to capture the roar of a lion with a microphone that can only pick up whispers. On the other hand, selecting an overly wide dynamic range for relatively low-intensity vibrations can lead to a decrease in sensitivity. It’s akin to using a microscope to read large print; you may miss finer details.
Automatic Adjustment of Anti-Aliasing Filters
To mitigate the challenges posed by aliasing due to insufficient sampling rates, most data collectors and analyzers incorporate anti-aliasing filters. These filters automatically adapt to changes in the sampling frequency, preventing aliasing and ensuring data integrity.
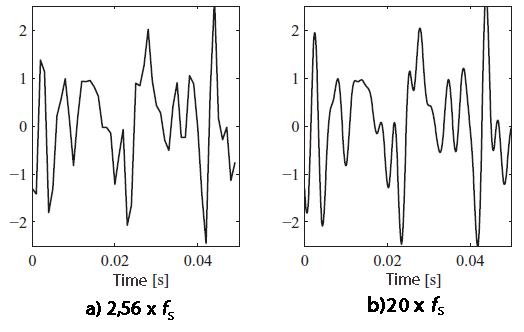
Fig. 4 Anti-aliasing filter operation
References
- C. Scheffer, P. GirdharMachinery Vibration Analysis & Predictive Maintenance(Oxford:Elsevier, 2004)
- A. Brandt, Noise and Vibration Analysis(New Delhi: Wiley, 2011)
- Bertoletti, 2020, Nyquist-Shannon Sampling Theorem
Frequently asked questions
What is the Nyquist-Shannon sampling theorem in vibration measurement?
The Nyquist-Shannon sampling theorem states that the sampling rate must be at least twice the highest frequency component in the analog signal (2×fmax). When this is respected, the sampled digital signal preserves all the information of the analog signal; half of the sampling frequency (fs/2) is called the Nyquist frequency.
What is aliasing in vibration measurement?
Aliasing occurs when the sampling frequency is lower than twice the highest frequency in the analog signal. Components above the Nyquist frequency are then folded back into the analyzed band, where they appear as false low-frequency peaks that cannot be distinguished from real ones, which can lead to misinterpretation of the vibration source. Analyzers use anti-aliasing filters to block those components before sampling and so prevent it.
How do anti-aliasing filters work in a vibration analyzer?
Anti-aliasing filters are low-pass electronic filters that let lower frequencies pass and block everything above half the sampling rate. They adjust automatically when the user changes the analyzer's frequency range, so the sampled data stays free of aliased components.
How do you choose the right dynamic range for vibration measurement?
Match the dynamic range to the expected vibration amplitude: a low range such as 2G for gentle vibrations and a higher range such as 8G or 16G for intense ones. A range that is too narrow clips the data and loses amplitude information, while a range that is too wide for small vibrations reduces sensitivity.
Why can different parts of the same machine need different measurement parameters?
Parts of one piece of equipment vibrate differently because of differences in shape, material and operating speed. In a conveyor with an electric motor and a reducer, the reducer output shaft and the motor produce quite different vibrations, so using the same measurement parameters on both can give incorrect results.
