Die Hüllkurvenanalyse, ein Schwerpunkt der Diagnostik, zielt auf Amplitudenschwankungen in Schwingungssignalen ab. Im Gegensatz zu herkömmlichen Methoden zeichnet es sich durch die Erkennung von Modulationen im Zusammenhang mit drohenden Fehlern wie Getriebeschäden oder Lagerdefekten aus. Durch die Untersuchung der Signalhüllkurven erhalten Wartungsteams einen erweiterten Überblick über den Maschinenzustand, was ein rechtzeitiges Eingreifen ermöglicht und die Gesamtzuverlässigkeit verbessert.
Grundlagen der Schwingungsanalyse
Vibrationssignale sind grundlegende Indikatoren für den Maschinenzustand und repräsentieren mechanische Bewegung. Diese Signale resultieren aus den dynamischen Wechselwirkungen innerhalb rotierender Maschinenkomponenten. Das Verständnis dieser Vibrationen ist für die Beurteilung des Zustands von Geräten von entscheidender Bedeutung. Vibrationssignale liefern Informationen über Frequenz, Amplitude und Phase der mechanischen Schwingungen und bilden die Grundlage für diagnostische Analysen.
Frequenzbereichsanalyse
Bei der Frequenzbereichsanalyse werden Schwingungssignale in ihre einzelnen Frequenzen zerlegt. Dieser Prozess enthüllt den spektralen Inhalt des Signals und identifiziert dominante Frequenzkomponenten. Zu den gängigen Werkzeugen für die Frequenzbereichsanalyse gehören Fourier-Transformationen und Spektralanalysen. Dieser Ansatz ist wertvoll, um bestimmte Schwingungsmuster zu lokalisieren, die mit Maschinenfehlern wie Unwuchten oder Fehlausrichtungen verbunden sind.
Zeitbereichsanalyse
Im Gegensatz dazu konzentriert sich die Zeitbereichsanalyse auf das Verhalten des Signals in der Zeitdimension. Es untersucht, wie sich das Vibrationssignal im Laufe der Zeit entwickelt, und liefert Einblicke in die zeitlichen Eigenschaften von Maschinenvibrationen. Zeitbereichstechniken wie Wellenformanalyse und statistische Messungen bieten ein umfassendes Verständnis des dynamischen Verhaltens der Maschine und helfen bei der Identifizierung vorübergehender Ereignisse und Unregelmäßigkeiten.
Einschränkungen traditioneller Analysemethoden
Herkömmliche Schwingungsanalysemethoden liefern zwar wertvolle Erkenntnisse, weisen jedoch Einschränkungen auf. Mit diesen Methoden kann es schwierig sein, Fehler im Frühstadium oder subtile, im Signal verborgene Anomalien zu erkennen, insbesondere in komplexen Industrieumgebungen mit hohem Hintergrundrauschen. Darüber hinaus mangelt es herkömmlichen Ansätzen möglicherweise an der erforderlichen Empfindlichkeit zur Identifizierung bestimmter Fehlertypen, was die Integration fortschrittlicherer Techniken wie der Hüllkurvenanalyse erforderlich macht.
Grundlagen der Hüllkurvenanalyse
Definition von Umschlag
Die Hüllkurve in der Signalverarbeitung bezieht sich auf eine Kurve, die die maximalen Amplitudenschwankungen eines Signals beschreibt. Im Zusammenhang mit der Maschinendiagnose stellt die Hüllkurve eine geglättete Version des Vibrationssignals dar, die Veränderungen der Amplitude im Laufe der Zeit hervorhebt. Es ist besonders hilfreich bei der Erfassung von Modulationen innerhalb des Signals, die mit verschiedenen Fehlern und Unregelmäßigkeiten verbunden sind.
Bedeutung bei der Identifizierung von Modulationen
Die Hauptbedeutung der Hüllkurve liegt in ihrer Fähigkeit, Modulationen innerhalb des Vibrationssignals zu erfassen. Modulationen sind periodische Schwankungen der Amplitude, die oft auf das Vorhandensein von Fehlern oder Anomalien in rotierenden Maschinen hinweisen. Die Hüllkurvenanalyse eignet sich hervorragend zur Isolierung dieser Modulationen und liefert eine klare und eindeutige Darstellung der zugrunde liegenden Fehlersignaturen, die im Rohschwingungssignal möglicherweise verdeckt sind.
Vergleich mit der Rohschwingungssignalanalyse
Der Vergleich der Hüllkurvenanalyse mit der herkömmlichen Rohschwingungssignalanalyse unterstreicht ihre Überlegenheit bei der Fehlererkennung. Während Rohsignale eine detaillierte, aber verrauschte Darstellung von Maschinenvibrationen bieten, bietet die Hüllkurvenanalyse eine verfeinerte, übergeordnete Perspektive. Durch die Fokussierung auf Amplitudenschwankungen filtert die Hüllkurvenanalyse effektiv irrelevante Details heraus und macht sie empfindlicher für subtile Änderungen im Zusammenhang mit sich entwickelnden Fehlern.
Vorteile der Hüllkurvenanalyse
Erhöhte Sensibilität: Die Hüllkurvenanalyse erhöht die Sensibilität für die Fehlererkennung im Frühstadium und ermöglicht es, Probleme zu erkennen, bevor sie eskalieren.
Effektiv in lauten Umgebungen: In industriellen Umgebungen mit erheblichem Hintergrundrauschen zeichnet sich die Hüllkurvenanalyse dadurch aus, dass sie fehlerbedingte Modulationen vom Umgebungsrauschen isoliert und so die Signalklarheit verbessert.
Vergrößerung der Fehlersignatur: Die Hüllkurvenanalyse fungiert als diagnostisches Vergrößerungsglas und verstärkt Fehlersignaturen, die im Rohsignal subtil oder maskiert sein können.
Proaktive Wartung: Die Fähigkeit, Fehler frühzeitig zu erkennen, ermöglicht eine proaktive Wartung, reduziert Ausfallzeiten und verlängert die Gesamtlebensdauer von Maschinen.
Signalerfassung und Vorverarbeitung
Signalkonditionierung und -verstärkung
Von Sensoren erfasste Rohsignale werden häufig einer Signalkonditionierung unterzogen, um sie für die Analyse vorzubereiten. Die Signalkonditionierung umfasst Prozesse wie Verstärkung, Analog-Digital-Wandlung und Filterung. Die Verstärkung erhöht die Stärke des Signals und stellt sicher, dass subtile Vibrationen nicht durch Rauschen überschattet werden. Eine ordnungsgemäße Signalaufbereitung ist für die Aufrechterhaltung der Signalintegrität während der gesamten Analyse von entscheidender Bedeutung.
Bedeutung der richtigen Sensorplatzierung
Die Platzierung von Vibrationssensoren ist ein entscheidender Faktor, der die Genauigkeit der Datenerfassung beeinflusst. Sensoren sollten strategisch positioniert werden, um Vibrationen zu erfassen, die in direktem Zusammenhang mit dem Zustand der Maschine stehen. Durch die richtige Platzierung der Sensoren wird sichergestellt, dass die erfassten Signale den Zustand wichtiger Komponenten wie Lager, Zahnräder oder rotierender Wellen genau widerspiegeln. Eine falsche Sensorplatzierung kann zu irreführenden oder unvollständigen Daten führen.
Filtertechniken zur Verbesserung der Hüllkurvenextraktion
Eine effektive Hüllkurvenextraktion basiert auf makellosen Signalen, weshalb die Filterung in der Vorverarbeitungsphase von entscheidender Bedeutung ist. Filtertechniken wie Bandpassfilter helfen dabei, bestimmte interessierende Frequenzbänder zu isolieren. Dieser Schritt ist besonders wichtig für die Hüllkurvenanalyse, da er die Extraktion von Modulationen im Zusammenhang mit Maschinenfehlern verbessert und gleichzeitig Störungen durch irrelevante Frequenzkomponenten oder Hintergrundgeräusche minimiert.
Signalkonditionierung und -verstärkung
Signalkonditionierung und -verstärkung
Von Sensoren erfasste Rohsignale werden häufig einer Signalkonditionierung unterzogen, um sie für die Analyse vorzubereiten. Die Signalkonditionierung umfasst Prozesse wie Verstärkung, Analog-Digital-Wandlung und Filterung. Die Verstärkung erhöht die Stärke des Signals und stellt sicher, dass subtile Vibrationen nicht durch Rauschen überschattet werden. Eine ordnungsgemäße Signalaufbereitung ist für die Aufrechterhaltung der Signalintegrität während der gesamten Analyse von entscheidender Bedeutung.
Bedeutung der richtigen Sensorplatzierung
Die Platzierung von Vibrationssensoren ist ein entscheidender Faktor, der die Genauigkeit der Datenerfassung beeinflusst. Sensoren sollten strategisch positioniert werden, um Vibrationen zu erfassen, die in direktem Zusammenhang mit dem Zustand der Maschine stehen. Durch die richtige Platzierung der Sensoren wird sichergestellt, dass die erfassten Signale den Zustand wichtiger Komponenten wie Lager, Zahnräder oder rotierender Wellen genau widerspiegeln. Eine falsche Sensorplatzierung kann zu irreführenden oder unvollständigen Daten führen.
Filtertechniken zur Verbesserung der Hüllkurvenextraktion
Eine effektive Hüllkurvenextraktion basiert auf makellosen Signalen, weshalb die Filterung in der Vorverarbeitungsphase von entscheidender Bedeutung ist. Filtertechniken wie Bandpassfilter helfen dabei, bestimmte interessierende Frequenzbänder zu isolieren. Dieser Schritt ist besonders wichtig für die Hüllkurvenanalyse, da er die Extraktion von Modulationen im Zusammenhang mit Maschinenfehlern verbessert und gleichzeitig Störungen durch irrelevante Frequenzkomponenten oder Hintergrundgeräusche minimiert.
Techniken zur Umschlagextraktion
Hilbert-Transformation und ihre Rolle in der Hüllkurvenanalyse
Die Hilbert-Transformation spielt eine zentrale Rolle bei der Hüllkurvenanalyse, indem sie eine Möglichkeit bietet, das analytische Signal aus einem reellwertigen Schwingungssignal zu extrahieren. Dies wird erreicht, indem die Phase des Originalsignals um 90 Grad verschoben wird, wodurch ein komplexes Signal erzeugt wird, das sowohl Amplituden- als auch Phaseninformationen enthält. Die Hüllkurve wird dann durch Berechnen der Größe dieses analytischen Signals ermittelt, wobei die zeitlichen Amplitudenschwankungen des Signals hervorgehoben werden.
Analytische Signaldarstellung
Die analytische Signaldarstellung umfasst sowohl das Originalsignal als auch seine Hilbert-Transformation und erzeugt so ein komplexes Signal, das eine umfassende Analyse von Amplitudenmodulationen ermöglicht. Durch die Einbeziehung sowohl realer als auch imaginärer Komponenten erfasst das Analysesignal die momentanen Amplituden- und Phaseneigenschaften des Vibrationssignals. Diese Darstellung ist entscheidend für die Erkennung von Modulationen, die auf Maschinenfehler hinweisen.
Demodulationstechniken
Demodulationstechniken werden eingesetzt, um die mit Maschinenfehlern verbundenen niederfrequenten Komponenten aus dem hochfrequenten Trägersignal zu isolieren. Durch die Demodulation des Analysesignals können Praktiker die Hüllkurve extrahieren und so effektiv die Amplitudenschwankungen hervorheben, die auf potenzielle Fehler hinweisen. Die Demodulation ist besonders wertvoll, um die fehlerbedingten Modulationen vom gesamten Vibrationssignal zu trennen.
Algorithmen zur Hüllkurvenextraktion (z. B. Empirical Mode Decomposition)
Bei der Hüllkurvenextraktion kommen häufig hochentwickelte Algorithmen zum Einsatz, wobei ein bemerkenswerter Ansatz die Empirical Mode Decomposition (EMD) ist. EMD zerlegt ein komplexes Signal in eine Reihe von intrinsischen Modusfunktionen (IMFs), die die Oszillationskomponenten des Signals auf verschiedenen Skalen darstellen. Aus diesen IMFs wird dann die Hüllkurve extrahiert, was eine detaillierte Analyse der mit bestimmten Fehlerfrequenzen verbundenen Amplitudenmodulationen ermöglicht.
Fehlersignaturen in der Hüllkurvenanalyse
Zahnradschaden und Modulationseffekte
Zahnschäden an Zahnrädern sind ein häufiges Problem bei rotierenden Maschinen und die Hüllkurvenanalyse erweist sich bei der Erkennung als äußerst effektiv. Wenn Zahnräder verschleißen oder beschädigt werden, treten Modulationen im Vibrationssignal bei Harmonischen der Zahneingriffsfrequenz auf. Die Hüllkurvenanalyse hebt diese Modulationen hervor und ermöglicht die frühzeitige Erkennung von Zahnschäden durch die charakteristischen Muster, die in der Hüllkurve beobachtet werden.
Lagerfehler und ihre Auswirkungen auf die Hülle
Lagerfehler wie Lochfraß oder Abplatzungen führen zu charakteristischen Modulationen im Schwingungssignal. Die Hüllkurvenanalyse verstärkt diese Modulationen und ermöglicht so die Identifizierung der spezifischen Frequenzen, die mit Lagerfehlern verbunden sind. Durch die Konzentration auf den Bereich können Analysten die frühen Stadien der Lagerverschlechterung lokalisieren, ein rechtzeitiges Eingreifen erleichtern und katastrophale Ausfälle verhindern.
Fehlausrichtung und ihre Manifestation im Umschlag
Eine Fehlausrichtung in rotierenden Maschinen verursacht Modulationen im Vibrationssignal bei Frequenzen, die mit der Drehzahl und der Fehlausrichtung selbst zusammenhängen. Die Hüllkurvenanalyse erkennt diese Modulationen und liefert einen klaren Hinweis auf Fehlausrichtungsprobleme. Durch die Identifizierung von Fehlausrichtungen mithilfe der Hüllkurvenanalyse können Wartungsteams das Problem umgehend beheben, weitere Schäden an Komponenten verhindern und die Maschinenleistung optimieren.
Andere häufige Fehler, die durch die Hüllkurvenanalyse erkannt werden
Unwucht: Unwucht rotierender Bauteile führt zu Modulationen im Schwingungssignal, insbesondere bei der Drehfrequenz. Die Hüllkurvenanalyse erhöht die Empfindlichkeit gegenüber diesen Modulationen und hilft so bei der Erkennung von Ungleichgewichtsproblemen.
Lockerheit: Lose Komponenten erzeugen Stoßkräfte, die zu Modulationen im Vibrationssignal führen. Die Hüllkurvenanalyse hilft dabei, diese Modulationen vom Hintergrundrauschen zu unterscheiden und erleichtert so die frühzeitige Erkennung von Lockerungen in Maschinen.
Probleme mit Riemen oder Kupplungen: Die Hüllkurvenanalyse ist wirksam bei der Erkennung von Fehlern im Zusammenhang mit Riemen oder Kupplungen, wie z. B. Schlupf oder Verschleiß. Die durch diese Probleme verursachten Modulationen werden im Umschlag hervorgehoben und ermöglichen eine gezielte Diagnose.
Fallstudie zur Hüllkurvenanalyse: Lagerausfall
Ein Ausfall von Lagern kann zu langfristigen Ausfallzeiten der gesamten Maschine und sogar der Produktionslinie führen. Da Lagerausfälle 41 % der Ausfallarten von Elektromotoren ausmachen und viel früher als ihre geschätzte Lebensdauer ausfallen, ist eine kontinuierliche Überwachung und Fehlervorhersage von Lagern eine große Notwendigkeit.
Der Betrieb von Maschinenkomponenten erzeugt immer Vibrationen. Lagerausfälle führen häufig zu veränderten Vibrationsmustern. Diese Vibrationen können mit Sensoren gemessen werden, die an den richtigen Stellen der Maschine angebracht sind. Die gemessenen Schwingungssignale werden digitalisiert und verarbeitet. Durch verschiedene Signalanalysetechniken können relevante Fehlersignalkomponenten extrahiert und untersucht werden. Auf diese Weise können Lagerfehler und Defekte erkannt und isoliert werden.
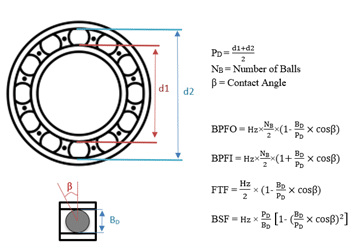
Das Wichtigste bei der Schwingungsanalyse ist die harmonische Analyse. Die Antriebsfrequenz und ihre Harmonischen werden anhand der Seitenbänder dieser Harmonischen analysiert. Sie stimmt jedoch nicht mit den exakten Vielfachen der Antriebsfrequenz bei Lagerausfällen überein. Abrieb in Lagern, der beispielsweise durch unzureichende Schmierung, falsche Montage oder Riffelung verursacht wird, erzeugt Vibrationen mit bestimmten Frequenzen. Da wir wissen, dass Lager aus vier grundlegenden mechanischen Teilen bestehen: Außenring, Kugel, Käfig und Innenring, weist jedes Teil seine eigene spezifische Ausfallhäufigkeit auf. Diese Fehlerfrequenzen sind BPFO (Ball Pass Frequency Outer), BSF (Ball Spin Frequency), FTF (Fundamental Train Frequency) und BPFI (Ball Pass Frequency Inner).
Band Auswahl
Es ist notwendig, einen Frequenzbereich im Schwingungsspektrum auszuwählen, in dem ein Lagerausfall auftritt, und alle Komponenten außerhalb des Bandes zu entfernen. Es wird davon ausgegangen, dass sich dieser ausgewählte Frequenzbereich nur auf Lagerausfälle und nicht auf andere Maschinenausfälle bezieht. Der optimale Bereich des Frequenzbandes, der die charakteristische Frequenz dieses Lagerausfalls mit der strukturellen Resonanz der Systeme kombiniert, kann auch manuell ausgewählt und in die inverse Fourier-Transformation eingegeben werden, und er kann auch mit spektraler Kurtosis, EMD (Empirical Mode) automatisiert werden Zerlegung) und andere Optimierungsalgorithmen.
Hüllkurvenspektrum
Das Signal wird moduliert, indem die Bandlücke ausgewählt wird, die charakteristische Frequenz des Lagerausfalls mit der strukturellen Resonanz der Systeme kombiniert wird und die inverse Fourier-Transformation durchgeführt wird. Anschließend wird das modulierte Signal in Zeitwellenform durch die Hilbert-Transformation umhüllt. Das Hüllkurvenspektrum wird durch erneute Fourier-Transformation des Hüllkurvensignals erhalten. Das vorherrschende Vorhandensein von Vibrationen bei den oben genannten Lagerausfallfrequenzen im Hüllkurvenspektrum weist auf einen Lagerausfall hin.
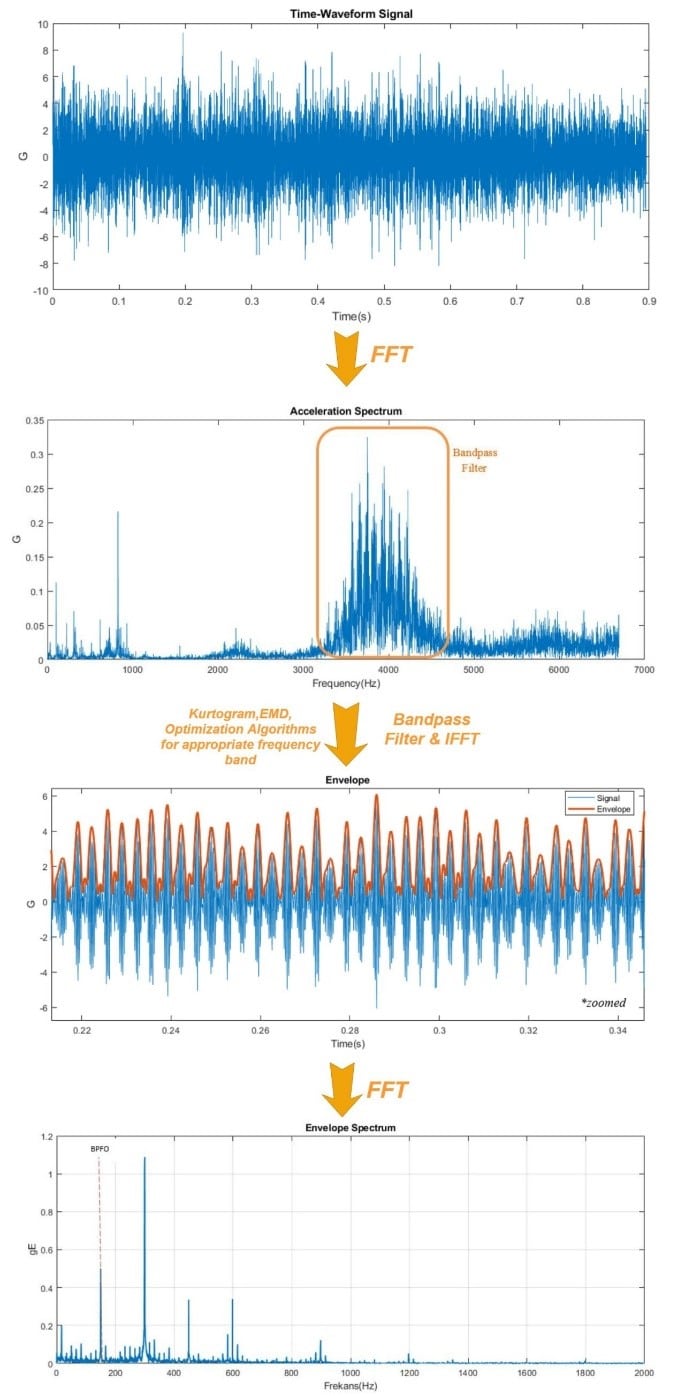
Abb. 1 Fehlermodusdiagramm
Abschluss
Basierend auf der Bewertung der Amplitudenmodulation zufälliger Vibrationen und struktureller Resonanz ist die Hüllkurvenanalyse eine der effektiven Möglichkeiten, den Zustand eines Lagers zu erkennen und zu bewerten. Die Verwendung der Hilbert-Transformation anstelle von Filterung und Korrektur bei der Hüllendetektion ermöglicht nicht nur Amplitudendemodulation für die Diagnose von Lagerfehlern, sondern auch Phasendemodulation und Frequenzdemodulation. Die Frequenzdemodulation ebnet den Weg für die Getriebediagnose und die Problembehebung von Problemen, die durch Torsionsschwingungen verursacht werden.
Weiterführende Literatur
Dezember 28, 2022
KI-gestützte Fehlerdiagnose mit Modusähnlichkeitsanalyse
AI can diagnose machine faults with vibration data but machine mode similarity analysis is an alternative, it uses…
September 15, 2022
Daten zu rotierenden Maschinen verstehen
Maschinendaten werden durch physische Attribute und Aktionen von Maschinen generiert, von Sensoren gesammelt und…
Mai 6, 2021
Was ist Cepstral-Analyse?
Die Cepstral-Analyse, ein Werkzeug zur Erkennung von Periodizität im Frequenzspektrum, kann bei der Erkennung von…
Oktober 9, 2020
Wie erfolgt die Fehlererkennung?
Vibrationsmessungen und -analysen unter Verwendung mehrerer Parameter können sich entwickelnde Probleme in Maschinen…
September 21, 2020
Parameterauswahl in der Vibrationsmessung
Vibrationsmessungen werden verwendet, um die Reaktion von Maschinen auf Kräfte zu bestimmen und potenzielle Probleme zu…
September 4, 2020
Was ist Schwingungsanalyse?
Um die Schwingungsanalyse zu verstehen, ist es wichtig, zunächst das Konzept der Schwingung selbst zu verstehen.…
Entdecken Sie unsere Produkte
Sensemore Lösung für vorausschauende Wartung
Wenn Ihnen dieser Blog gefallen hat, erkunden Sie unsere Seite zur vorausschauenden Wartungslösung.